Abstract

Context: The differentiated papillary and follicular thyroid neoplasms can be characterized from the notions of fractal and Euclidean geometry to overcome the challenges faced by the pathologist. This method was previously used in differentiating preinvasive lesions of cervical cancer. Aims: to characterize the irregularity of histologic samples of normal thyroid cells as well as benign and malignant thyroid papillary and follicular carcinomas, through the box-counting method using the principles of fractal and Euclidian geometry. Settings and Design: This is a retrospective study involving the measurement of thyroid cells through pixels in photographs, applying geometric methods. Subjects and Methods: Photographs of histological samples from normal and neoplastic biopsy samples were taken and processed by a software in order to delimit the borders of the nucleus and cytoplasm. Then, the box-counting method was applied by superimposing grids of 5 and 10 pixels to measure the fractal dimension and the occupied spaces of the cellular surface. Results: The set of papillary and follicular cells evaluated from the occupied spaces from the borders and surfaces of the nucleus and cytoplasm in the 5-pixel grid showed that normal cells are included within a range of values, while the neoplastic variations are differentiable from this range. Conclusions: Fractal and Euclidean geometries can differentiate normality from some benign and malignant thyroid lesions, which opens a path to develop methodologies that characterize more precisely distinctive features between normal and neoplastic cells independent of qualitative criteria from traditional pathology and histology.

Keywords

Cell nucleus - cytoplasm - fractal - histology - pathology

Publication History

Received: 27 September 2020

Accepted: 23 August 2020

Article published online:
14 May 2021

© 2020. Indian Society of Medical and Paediatric Oncology. This is an open access article published by Thieme under the terms of the Creative Commons Attribution-NonDerivative-NonCommercial-License, permitting copying and reproduction so long as the original work is given appropriate credit. Contents may not be used for commercial purposes, or adapted, remixed, transformed or built upon. (https://creativecommons.org/licenses/by-nc-nd/4.0/.)

Thieme Medical and Scientific Publishers Pvt. Ltd.
A-12, 2nd Floor, Sector 2, Noida-201301 UP, India

Abstract

Keywords

Cell nucleus - cytoplasm - fractal - histology - pathology

Introduction

The American Cancer Association estimated 52.070 new cases of thyroid neoplasms and 2.170 deaths due to these diseases for 2019 in the United States. Although constant, the mortality rate for thyroid cancer is low compared to other types of neoplasms.[1] The introduction and routine usage of ultrasound resulted in the detection of small nodules and thus contributing to the increased incidence of thyroid cancers.[1] It is worth noting that better diagnostic methods are resulting in early diagnosis and diagnosis of advanced stage cancer, independent of the type of cancer.[2]

In the clinical literature, it is documented that the majority of thyroid neoplasms begin in follicular cells of the thyroid gland and their progression varies from well-differentiated thyroid cancers to anaplastic cancers.[3],[4] There are different types of malignant thyroid neoplasms depending on the cell of origin and the extent of differentiation, or if they are medullar or anaplastic.[5] Differentiated thyroid neoplasms include papillary, follicular, and Hürthle cell cancer; most differentiated tumors are heterogeneous, including papillary and follicular patterns simultaneously, which was formerly described as mixed follicular and papillary carcinomas.[3] However, the current classifications differentiate among the most predominant histological pattern within differentiated thyroid carcinomas, establishing variants of papillary carcinoma.[3] Nevertheless, it has been considered that differentiated neoplastic cells share similar morphologic features with normal cells when under microscopy.[5]

The initial diagnostic criteria of the papillary carcinoma were established through a growth pattern; then, the shape of the nucleus was more relevant, given that the nuclear characteristics are considered as a diagnostic pattern of the tumor.[6] Studies conducted to evaluate the shape of the nucleus of papillary tissues have found that this structure is bigger and oval shaped when compared to the nucleus of benign follicular cells, although it is common to find similar nuclear features.[6] Thus, the necessity for modalities that can differentiate the features at ultrastructural level has arisen, in which an extreme polymorphism in the nucleus of differentiated thyroid carcinomas has been found, some presenting spherical forms sliced by a deep narrow furrow in two unequal parts or the appearance of ground-glass, among other features.[7]

Fractal irregular objects that are the base of fractal geometry[8],[9] and its notions have been applied for the characterization of irregular structures of the human body, revealing the possibility of developing more precise measures of the irregularity of these structures.[10],[11],[12],[13],[14],[15],[16],[17],[18],[19],[20],[21] Among the designed methods to evaluate the degree of irregularity of fractal objects, the Box-Counting method is found. This method evaluates fractal dimension of fractal objects called wild fractals[8],[9] such as coronary arteries[14] and has been applied to clinically characterize and diagnose glaucoma, the normal human vasculature, breast cancer tissues, and others.[18],[19],[20] From this line of investigation, different diagnostic methodologies of clinical application that evaluate the different lesions of cervical cells have been developed capable of differentiating benign from malignant atypical squamous cells of undetermined significance relying on the occupied spaces of the nucleus and cytoplasm.[16]

Considering that thyroid cells exhibit irregular features suggesting their fractality and in the frame of previous research, the purpose of this study is to conduct an application of a methodology developed by Rodríguez with the purpose of characterizing the irregularity of the nucleus and cytoplasm of cells obtained from biopsy samples of normal and benign and malignant papillary and follicular thyroid neoplasms through the box-counting method and to compare the values of the occupied spaces of the surface and border of these structures.

Subjects and Methods

Surface of the object

Quantity of pixels occupied by the cytoplasm or nucleus.

Border of the object

Quantity of pixels occupied by the edges of the cytoplasm or nucleus.

Fractal dimension

Evaluates the degree of irregularity of fractal objects, which are both the cytoplasm and the nucleus of cells, through the following formula:

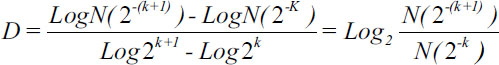
| Figure.1:

Where D: Fractal dimension; N: Quantity of spaces occupied by the surface or the border of the fractal objects; and k, the partition of the grid.

Population

Histological samples prepared with quality and staining criteria were obtained from biopsy samples of patients with different sex and ages who had indication of thyroid gland biopsy. From these samples, different sets of cells were organized and observed, considering normal thyroid cells as well as benign and malignant thyroid papillary and follicular carcinomas according to the traditional evaluation performed by an expert pathologist like this: 2 sets of 10 normal papillary and follicular cells; 2 sets of 10 cells with adenoma and follicular carcinoma; and 4 sets of 10 cells with papillary thyroid carcinoma classical variant, poorly differentiated papillary carcinoma, anaplastic thyroid carcinoma with one nucleus, and anaplastic thyroid carcinoma with 2 or more nuclei.

Procedure

The histological samples were observed with a light microscope using transmitted moderately intense light under oil immersion at a magnification of ×100 and were then photographed with a digital camera. All the photographs were adjusted to be saved with the same width in pixels, and the borders of the cytoplasm and nucleus of each cell were defined with an image editor. Then, these images were treated with a software designed in C++ that recognizes these edges and allows to measure the structures.

In order to find the fractal dimension of each cell (Equation 1), two grids of 5 (R5) and 10 (R10) pixels are overlapped on the images. Then, a quantification of the squares occupied by the border and the surface of each cell was done. The measurement of the number of squares occupied by the surface of the cell with the R5 and R10 grids allows to obtain fractal dimension. Spaces occupied by the borders of the objects were as well considered for measurement.

Ethical aspects

As the samples were obtained from patients who had a medical indication of thyroid biopsy, consent was taken from patients in order to authorize the processing of their samples for research purposes. The integrity and anonymity of the participants was preserved at all times. The Institutional Ethics Committee of Fundación Universitaria Autónoma de las Américas approved the development of the project. According to the article 11 of the Resolution 8430 of 1993 and the law 84 of 1989 emitted by the Ministerium of Health, the kind of risk related to this research is minimum, since physical and mathematical calculations are performed over results.

Results

[Table 1] and [Table 2] display the histopathological diagnosis for the group of follicular and papillary cells as well as the values of the spaces occupied in R5 and R10 grids. Values of fractal dimension were not considered in the characterization of cells due to overlapping of numbers. The analysis of normal cells highlights that the number of squares occupied when overlapping the two grids, both the surface and cytoplasm overlap. Besides, it was noted that the nucleus and cytoplasm of normal papillary tissues had bigger occupied spaces, consistent with other studies.[6]

Table 1
Drugs
Number	Follicular thyroid cells
	Histopathological diagnostic	Nucleus					Cytoplasm
	Histopathological diagnostic	R5	R10	S	Con	Df	R5	R10	S	Con	Df
Ca – Carcinoma
1	Normal	54	27	2088	194	1	115	46	1473	464	1.322
2	Normal	47	25	2099	183	0.911	120	51	1752	448	1.234
3	Normal	38	19	1404	134	1	121	55	3025	455	1.138
4	Normal	24	12	736	92	1	94	40	1884	366	1.233
5	Normal	34	19	1394	127	0.840	144	68	3370	549	1.082
6	Follicular adenoma	33	17	1297	134	0.957	85	36	1611	363	1.239
7	Follicular adenoma	37	20	1339	134	0.888	68	32	1204	298	1.087
8	Follicular adenoma	38	20	1835	161	0.926	63	32	1468	261	0.977
9	Follicular adenoma	33	17	1515	144	0.957	78	31	928	330	1.331
10	Follicular adenoma	37	19	1755	148	0.962	81	33	1344	313	1.295
11	Follicular Ca.	47	23	2025	191	1.031	124	59	3178	544	1.072
12	Follicular Ca.	52	26	2960	199	1	139	66	4128	555	1.075
13	Follicular Ca.	38	20	1146	157	0.926	98	40	1471	420	1.293
14	Follicular Ca.	42	22	1600	169	0.933	112	50	2583	458	1.163
15	Follicular Ca.	41	22	1709	164	0.898	117	57	3527	486	1.037

Table 2
Histopathological diagnostics and values of representative papillary thyroid cells

Furthermore, it can be observed that the differences of the spaces occupied when overlapping the two grids in the variations of the nucleus of the of the other cellular groups with regard to normal cells were quite small. The values for normal follicular thyroid cells varied between 38–26 and 19–12 with the R5 and R10 grids, while these values were 42–33 and 23–16 for normal papillary thyroid cells, respectively. With respect to the cytoplasm, slight changes are noted with respect to all the cellular groups when compared with the normal group of follicular and papillary tissues, which were 144–89 and 132–84, respectively.

In exchange, the values of the surfaces and borders allow further characterization between the groups of follicular and papillary tissues. For example, the nuclear surface of normal follicular cells varied between 1404 and 502 while adenoma cells varied between 1835 and 1297 and follicular carcinoma cells varied between 2960 and 1146. This indicates that the nuclear surface of follicular carcinoma is bigger than for normal tissues; similar findings are obtained when analyzing the values of the borders. The values of the surface of the cytoplasm of papillary normal cells varied between 3370 and 1526, whereas follicular adenoma cell varied between 1611 and 928, and follicular carcinoma occupies a bigger space.

Discussion

This is the first investigation that conducts an application of a methodology based on the notions of fractal and Euclidean geometry in order to characterize different groups of follicular and papillary thyroid cells, through the analysis of the degree of irregularity of the cellular surfaces and borders. The results of the evaluated groups with the box-counting method reveal the possibility of obtaining new methods of characterization from the occupied spaces by the nucleus and cytoplasm.

In the medical literature, it is mentioned that well-differentiated thyroid carcinomas, whether papillary or follicular, are morphologically similar to normal tissues under microscopy.[5] This study found that the values of the occupied spaces with the two grids in normal follicular and papillary cells are overlapped, but papillary cells are slightly bigger. Although these results are consistent with some clinical results,[6] the measurements developed from the values of the surface and border of cells reveal the possibility of enhancing the distinctions between these cellular groups, which in the future can contribute to the design of a complementary diagnostic methodology for thyroid cancer.

On the other hand, cervical cancer has been analyzed under this line of investigation, achieving the development of diagnostic methodologies with which is possible to conduct objective and reproducible characterizations of preneoplastic and neoplastic states.[15],[16],[18] This research highlights as well that current oncologic knowledge can further be amplified with methodologies that measure cellular structures and establish mathematical numerical values that allow diagnose cellular lesions.

The development of precise methodologies that reduce the inter- and intraobserver diagnostic variability has been a priority in medicine to ensure clearer diagnostics. This has been achieved through the theoretical physics and mathematical thinking that seeks to generalize phenomena, independent of risk factors or the experience of the operator. For example, the studies developed in neonatal, fetal, and adult cardiology are proof of the applicability of this thinking, from which alterations of cardiac dynamics and mortality can be predicted.[22],[23],[24]

Limitations

This study and other methods,[22],[23],[24] although highly promising in the clinical context, can only be clinically applicable if automatized through specialized software that allows to obtain immediate diagnostics. Furthermore, the acausal perspective of this research does not answer causal relationship among phenomena, which is why this evaluation must be complemented with other methods that elucidate the etiology of diseases.

Conclusions

A novel method based on fractal and Euclidean geometries was used to characterize thyroid cellular features. This method could enhance the diagnosis of thyroid cancer since it is independent of the operator diagnostic criteria and expertise; however, diagnostic parameters must be first established in other diagnostic agreements studies between this method and the current histopathological criteria with larger samples that confirm our findings. Furthermore, this method must be fully automated since the application performed in this study was manual.

Acknowledgment

We thank Visión de las Américas Universitary Foundation for their support to our investigations, specially to the department of Research of the university and the Faculty of Medicine for the financial support provided through the project P126-2018. Special thanks to doctors Verónica García Maya, Research director, Edwin Meneses, director of the group “investigación en salud y comunidad,” and doctor Mauricio Hidelberg Montoya, dean of the Faculty of Medicine for their support to our investigations.

Conflict of Interest

There are no conflicts of interest.

References

American Cancer Society. Key Statistics for Thyroid Cancer. 2019. Available from: https://www.cancer.org/cancer/thyroidcancer/ about/key statistics.html. [Last accessed 2019 Sep 12].

Sherma S. Thyroid carcinoma. Lancet 2003; 361: 501-11

Shah JP. Thyroid carcinoma: Epidemiology, histology, and diagnosis. Clin Adv Hematol Oncol 2015; 13: 3-6

Wreesmann VB, Ghossein RA, Patel SG, Harris CP, Schnaser EA, Shaha AR. et al. Genome-wide appraisal of thyroid cancer progression. Am J Pathol 2002; 161: 1549-56

American Cancer Society. Qué es el Cáncer de Tiroides? 2019. Available from: https://www.cancer.org/es/cancer/cancer-detiroides/acerca/que-es-cancer-de-tiroides.html. Last accessed 2019 Sep 12]

Kunjumon DT, Upadhyaya K. Histopathological features of papillary thyroid carcinoma with special emphasis on the significance of nuclear features in their diagnosis. Arch Med Health Sci 2014; 2: 16-22

Beaumont A, Ben Othman S, Fragu P. The fine structure of papillary carcinoma of the thyroid. Histopathology 1981; 5: 377-88

Mandelbrot B. How long is the coast of Britain?. Science 1967; 156: 636-8

Peitgen J. Length area and dimension. Measuring complexity and scalling properties. In: Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag; 1992. p. 183-228

Baish JH, Jain R. Fractals and cancer. Cancer Res 2000; 60: 3683-8

Pohlman S, Powell KA, Obuchowski NA, Chilcote WA, Grundfest-Broniatowski S. Quantitative classification of breast tumors in digitized mammograms. Med Phys 1996; 23: 1337-45

Lefebvre F, Benali H, Kahn E, Di Paola R. A fractal approach to the segmentation of microcalcifications in digital mammograms. Med Phys 1995; 22: 381-90

Luzi P, Bianciardi G, Miracco C, De Santi MM, Del Vecchio MT, Alia L. et al. Fractal analysis in human pathology. Ann N Y Acad Sci 1999; 879: 255-7

Rodríguez JO, Prieto SE, Correa C, Bernal PA, Puerta GE, Vitery S. et al. Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Med Phys 2010; 10: 1

Prieto Bohórquez SE, Velásquez JO, Correa HerreraSC, Soracipa MuñozMY. Diagnosis of cervical cells based on fractal and Euclidian geometrical measurements: Intrinsic geometric cellular organization. BMC Med Phys 2014; 14: 2

Velásquez JO, Bohórquez SE, Herrera SC, Cajeli DD, Velásquez DM, de Alonso MM. Geometrical nuclear diagnosis and total paths of cervical cell evolution from normality to cancer. J Cancer Res Ther 2015; 11: 98-104

Rodríguez J, Moreno N, Alfonso D, Méndez M, Flórez A. Geometrical Characterization of Morphology Equinocyte. Arch Med 2017; 13: 1-5

Lamani D, Ramegowda DR, Manjunath DR. Fractal dimension as diagnostic parameter to detect glaucoma. Int J Innov Eng Technol 2013; 2: 63-9

Jelinek H, de Mendonça M, Oréfice F, Garcia C, Nogueira R, Soares J. et al. Fractal analysis of the normal human retinal vasculature. Int J Ophthalmol Vis Sci 2009; 8: 1-5

George LE, Mohammed EZ. Cancer Tissues Recognition System using Box Counting Method and Artificial Neural Network.International Conference of Soft Computing and Pattern Recognition; 2011

Rodríguez J, Prieto S, Tabares L, Rubiano A, Prieto I, Domínguez D. et al. Simulations of cervical cells from normal to atypical squamous cells of undetermined significance (ASCUS) with fractal geometry. Rev UDCA Act Div Cient 2013; 16: 303-11

Rodríguez J. New physical and mathematical diagnosis of fetal monitoring: clinical application prediction. Momento Revista de Física 2012; 44: 49-65

Rodríguez J, Prieto S, Flórez M, Alarcón C, López R, Aguirre G. et al. Physical-mathematical diagnosis of cardiac dynamic on neonatal sepsis: predictions of clinical application. J Med Med Sci 2014; 5: 102-8

Rodríguez J. Dynamical systems applied to dynamic variables of patients from the intensive care unit (ICU). Physical and mathematical mortality predictions on ICU. J Med Med Sci 2015; 6: 102-8

Address for correspondence

Dr. Javier Oswaldo Rodríguez

Cra. 79B N° 51-16 Sur. Int

5. Apt. 102, Kennedy, Bogotá

Colombia

Email: grupoinsight2025@gmail.com

Publication History

Received: 27 September 2020

Accepted: 23 August 2020

Article published online:
14 May 2021

© 2020. Indian Society of Medical and Paediatric Oncology. This is an open access article published by Thieme under the terms of the Creative Commons Attribution-NonDerivative-NonCommercial-License, permitting copying and reproduction so long as the original work is given appropriate credit. Contents may not be used for commercial purposes, or adapted, remixed, transformed or built upon. (https://creativecommons.org/licenses/by-nc-nd/4.0/.)

Thieme Medical and Scientific Publishers Pvt. Ltd.
A-12, 2nd Floor, Sector 2, Noida-201301 UP, India
Number	Follicular thyroid cells
	Histopathological diagnostic	Nucleus					Cytoplasm
	Histopathological diagnostic	R5	R10	S	Con	Df	R5	R10	S	Con	Df
Ca – Carcinoma; Pa – Papillary; Pd – Poorly-differentiated; An – Anaplastic; M – Multinucleate
1	Pa. thyroid Ca. classical variant	46	24	2233	138	0.939	112	48	2248	450	1.222
2	Pa. thyroid Ca. classical variant	47	25	2391	196	0.911	124	59	2918	510	1.072
3	Pa. thyroid Ca. classical variant	39	18	2045	158	1.115	99	45	1820	410	1.138
4	Pa. thyroid Ca. classical variant	38	20	1857	162	0.926	93	42	1699	416	1.147
5	Pa. thyroid Ca. classical variant	45	21	2125	171	1.100	104	46	2144	407	1.177
6	Pd. Pa Ca.	43	22	2461	177	0.967	118	60	3665	502	0.976
7	Pd. Pa Ca.	51	25	2977	200	1.029	124	60	2773	519	1.047
8	Pd. Pa Ca.	46	23	2237	188	1	139	62	3552	551	1.165
9	Pd. Pa Ca.	37	19	1394	147	0.962	107	53	3440	441	1.014
10	Pd. Pa Ca.	47	25	2489	190	0.911	119	54	2309	482	1.140
11	An. thyroid Ca.	28	14	802	107	1	78	34	1331	308	1.198
12	An. thyroid Ca.	43	21	1442	157	1.034	136	63	3720	519	1.110
13	An. thyroid Ca.	37	20	1086	139	0.888	106	49	2274	433	1.113
14	An. thyroid Ca.	22	10	686	96	1.138	74	31	1613	320	1.255
15	An. thyroid Ca. M	41	21	2247	160	0.965	246	121	25476	936	1.024
16	An. thyroid Ca. M	37	20	1407	147	0.888	243	123	26396	920	0.982
17	An. thyroid Ca. M	35	19	1105	128	0.881	233	115	26714	902	1.019
18	An. thyroid Ca. M	40	20	2015	155	1.000	243	120	25741	929	1.018
19	An. thyroid Ca. M	25	11	481	85	1.184	228	116	27516	859	0.975

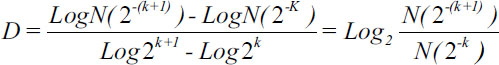
| Figure.1:

References

American Cancer Society. Key Statistics for Thyroid Cancer. 2019. Available from: https://www.cancer.org/cancer/thyroidcancer/ about/key statistics.html. [Last accessed 2019 Sep 12].
Sherma S. Thyroid carcinoma. Lancet 2003; 361: 501-11
Shah JP. Thyroid carcinoma: Epidemiology, histology, and diagnosis. Clin Adv Hematol Oncol 2015; 13: 3-6
Wreesmann VB, Ghossein RA, Patel SG, Harris CP, Schnaser EA, Shaha AR. et al. Genome-wide appraisal of thyroid cancer progression. Am J Pathol 2002; 161: 1549-56
American Cancer Society. Qué es el Cáncer de Tiroides? 2019. Available from: https://www.cancer.org/es/cancer/cancer-detiroides/acerca/que-es-cancer-de-tiroides.html. Last accessed 2019 Sep 12]
Kunjumon DT, Upadhyaya K. Histopathological features of papillary thyroid carcinoma with special emphasis on the significance of nuclear features in their diagnosis. Arch Med Health Sci 2014; 2: 16-22
Beaumont A, Ben Othman S, Fragu P. The fine structure of papillary carcinoma of the thyroid. Histopathology 1981; 5: 377-88
Mandelbrot B. How long is the coast of Britain?. Science 1967; 156: 636-8
Peitgen J. Length area and dimension. Measuring complexity and scalling properties. In: Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag; 1992. p. 183-228
Baish JH, Jain R. Fractals and cancer. Cancer Res 2000; 60: 3683-8
Pohlman S, Powell KA, Obuchowski NA, Chilcote WA, Grundfest-Broniatowski S. Quantitative classification of breast tumors in digitized mammograms. Med Phys 1996; 23: 1337-45
Lefebvre F, Benali H, Kahn E, Di Paola R. A fractal approach to the segmentation of microcalcifications in digital mammograms. Med Phys 1995; 22: 381-90
Luzi P, Bianciardi G, Miracco C, De Santi MM, Del Vecchio MT, Alia L. et al. Fractal analysis in human pathology. Ann N Y Acad Sci 1999; 879: 255-7
Rodríguez JO, Prieto SE, Correa C, Bernal PA, Puerta GE, Vitery S. et al. Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Med Phys 2010; 10: 1
Prieto Bohórquez SE, Velásquez JO, Correa HerreraSC, Soracipa MuñozMY. Diagnosis of cervical cells based on fractal and Euclidian geometrical measurements: Intrinsic geometric cellular organization. BMC Med Phys 2014; 14: 2
Velásquez JO, Bohórquez SE, Herrera SC, Cajeli DD, Velásquez DM, de Alonso MM. Geometrical nuclear diagnosis and total paths of cervical cell evolution from normality to cancer. J Cancer Res Ther 2015; 11: 98-104
Rodríguez J, Moreno N, Alfonso D, Méndez M, Flórez A. Geometrical Characterization of Morphology Equinocyte. Arch Med 2017; 13: 1-5
Lamani D, Ramegowda DR, Manjunath DR. Fractal dimension as diagnostic parameter to detect glaucoma. Int J Innov Eng Technol 2013; 2: 63-9
Jelinek H, de Mendonça M, Oréfice F, Garcia C, Nogueira R, Soares J. et al. Fractal analysis of the normal human retinal vasculature. Int J Ophthalmol Vis Sci 2009; 8: 1-5
George LE, Mohammed EZ. Cancer Tissues Recognition System using Box Counting Method and Artificial Neural Network.International Conference of Soft Computing and Pattern Recognition; 2011
Rodríguez J, Prieto S, Tabares L, Rubiano A, Prieto I, Domínguez D. et al. Simulations of cervical cells from normal to atypical squamous cells of undetermined significance (ASCUS) with fractal geometry. Rev UDCA Act Div Cient 2013; 16: 303-11
Rodríguez J. New physical and mathematical diagnosis of fetal monitoring: clinical application prediction. Momento Revista de Física 2012; 44: 49-65
Rodríguez J, Prieto S, Flórez M, Alarcón C, López R, Aguirre G. et al. Physical-mathematical diagnosis of cardiac dynamic on neonatal sepsis: predictions of clinical application. J Med Med Sci 2014; 5: 102-8
Rodríguez J. Dynamical systems applied to dynamic variables of patients from the intensive care unit (ICU). Physical and mathematical mortality predictions on ICU. J Med Med Sci 2015; 6: 102-8

IJMPO Indian Journal of Medical and Paediatric Oncology.

Year (Archive)

Year

Issues

Search

Recent Articles

IJMPO—A Journey of a Thousand Miles

Coronavirus Disease 2019 Treatment—T-Cells Hold the Key in Severe Cases

Why Is China Importing COVID-19 Vaccine Now?

Application of Fractal and Euclidean Methods to Differentiate Normal and Neoplastic Thyroid Cells

Abstract

Keywords

Publication History

Abstract

Keywords

Introduction

Subjects and Methods

Surface of the object

Border of the object

Fractal dimension

Population

Procedure

Ethical aspects

Results

Discussion

Limitations

Conclusions

Acknowledgment

Conflict of Interest

References

Address for correspondence

Publication History

References

CONTACT US

QUICK LINKS

NEWSLETTER

IJMPO Indian Journal of Medical and Paediatric Oncology